4. LOS TEOREMAS EN MATEMÁTICA - PARTE 2

2. Absurdos, contraejemplos y otras formas de demostrar

Hemos visto que la demostración de la validez de la fórmula resolvente de cuadráticas es una demostración constructiva. Otro ejemplo de esto es la fórmula para la suma de los primeros $n$ números naturales:

Proposición. Si se quieren sumar los primeros $n$ números naturales, podemos utilizar la siguiente fórmula:

$1 + 2 + 3 + \dots + n = \frac{n(n+1)}{2}$

Antes de demostrar esta proposición, veamos un ejemplo de uso de esta fórmula. Si se quieren sumar los números del 1 al 10 podemos hacer:

$\frac{10 \cdot (10+1)}{2} = 55$

Demostración. Organicemos la suma de los números de 1 hasta n de la siguiente manera:

La primera fila tiene una unidad, la segunda 2, la tercera 3, y así hasta la última, que tiene $n$ unidades. Si duplicamos esta cantidad podemos organizar sus unidades así:

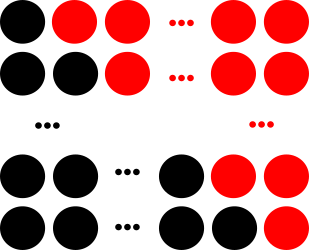
Queda así un rectángulo formado por $n$ filas de $n+1$ unidades; de modo que en total hay $n(n+1)$ unidades. Luego el número $1 + 2 + \dots + n$ tendrá la mitad de este valor, es decir, $\frac{n(n+1)}{2}$ . Q.E.D.

4.1 Demostraciones por el absurdo

Otro tipo de demostración son las demostraciones por el absurdo.

Fuente: Matemática 4 (De Simone, I. y Turner, M.)

¿Cuál es la idea de una demostración por el absurdo? Se comienza suponiendo que la tesis no se cumple (en este caso, que $\sqrt{2}$ es un número racional). Luego se realizan derivaciones lógicas hasta llegar a un absurdo. De tal modo, no queda otra alternativa que concluir que la premisa inicial (la tesis no se cumple) es falsa.

4.2 Contraejemplos

Algunas demostraciones utilizan la búsqueda de contraejemplos. Un contraejemplo es un ejemplo que da cuenta de la falsedad de una proposición. Por ejemplo:

Proposición. Dados $a$ y $b$ distintos de cero, se verifica:

$(a+b)^2 \neq a^2 + b^2 \quad \forall a,b \neq 0$

Demostración. Si suponemos que la igualdad es verdadera, debería cumplirse para cualquier par de números $a$ y $b$ . Pero si $a = 3$ y $b = 4$ , sucede que $(3+4)^2 = 49 \neq 3^2 + 4^2 = 25$ . Es interesante observar que si tomamos $a = 0$ o $b = 0$ , la igualdad se verifica; sin embargo, un ejemplo no garantiza la inexistencia de contraejemplos.