2. LAS DEFINICIONES EN MATEMÁTICA
| Sitio: | Campus Claves Académica |
| Curso: | Lenguaje matemático - EnlaceUBA |
| Libro: | 2. LAS DEFINICIONES EN MATEMÁTICA |
| Imprimido por: | Invitado |
| Día: | domingo, 15 de febrero de 2026, 12:04 |
1. Las definiciones en matemática
Durante el transcurso de la escuela secundaria, la enseñanza de funciones ocupa un lugar central en las clases de matemática. Un libro que suele ser utilizado para la enseñanza de estos contenidos en la universidad es Cálculo diferencial e integral, de N. Piskunov. Veamos qué nos dice este texto acerca de las funciones:

Fuente: Piskunov, N. (1980)
En la página 14 hay un título conocido: “Función”. El texto empieza con una introducción, un ejemplo, y luego aparecen dos pequeños apartados titulados “Definición 1” y “Definición 2”. Al leerlas con atención veremos que en la primera definición se explica qué se entiende por variable independiente, variable dependiente y relación funcional. En la segunda, se define qué es el dominio de una función.
¿Qué rol juegan las definiciones en la matemática? Las definiciones son secciones en las que se introducen de manera precisa los objetos, operaciones o cualquier otro tipo de elementos necesarios para el desarrollo de los conceptos de la teoría. En matemática es importante tener bien determinados los objetos para que no haya ambigüedades. Estas secciones en general están anunciadas (con la palabra “Definición”) o recuadradas. A partir de una definición podemos evaluar si un objeto cumple o no con ella, y decidir si ese objeto puede o no ser llamado con el nombre dado en la definición.
De acuerdo a la definición de función podemos decir, por ejemplo, que la relación  es una relación funcional entre las variables
es una relación funcional entre las variables  e
e  , y que la variable independiente es
, y que la variable independiente es  , en tanto que la dependiente es
, en tanto que la dependiente es  , ya que para cada valor de
, ya que para cada valor de  se determina, con la fórmula, un único valor de
se determina, con la fórmula, un único valor de  . Del mismo modo, la relación
. Del mismo modo, la relación  , no es una relación funcional entre
, no es una relación funcional entre  e
e  , pues a cada valor de
, pues a cada valor de  no corresponde solo un valor de
no corresponde solo un valor de  . Por ejemplo, para
. Por ejemplo, para  , la ecuación se satisface con
, la ecuación se satisface con  ó
ó  porque
porque  . ¿Será una relación funcional entre
. ¿Será una relación funcional entre  y
y  ? Tampoco, ya que para
? Tampoco, ya que para  , podremos tomar tanto
, podremos tomar tanto  como
como  .
.
2. Explorando más definiciones
En esta sección vamos a analizar algunos tipos de definiciones que son frecuentes tanto en los textos que se utilizan en los últimos años de la escuela secundaria como en los primeros años de la universidad.
2.1 Definiciones con cuantificadores
En algunas definiciones aparecen cuantificadores, en tanto que en otras no (o al menos, no explícitamente). Veamos un ejemplo:
Definición. Todo número entero  se dice par si existe algún entero se dice par si existe algún entero  tal que tal que  . . |
Vemos que aquí aparece un cuantificador: “existe algún”. Tratemos de comprender cómo funciona esta condición de existencia a partir de algunos ejemplos:
- ¿Será par, a partir de la definición, el número
 ?
? - ¿El
 es par? ¿Y el
es par? ¿Y el  ?
? - ¿Podemos considerar que el
 es par?
es par?
Como  , concluimos que es par, ya que existe un entero,
, concluimos que es par, ya que existe un entero,  , que al multiplicarse por
, que al multiplicarse por  , da
, da  .
.
Para el  , no existe un valor de
, no existe un valor de  tal que
tal que  (dejamos al lector convencerse de su inexistencia).
(dejamos al lector convencerse de su inexistencia).
El entero negativo  es par, ya que al tomar
es par, ya que al tomar  , se cumple la condición de paridad.
, se cumple la condición de paridad.
Por último,  no es par. ¿Por qué? Porque no cumple la premisa inicial: “todo número entero
no es par. ¿Por qué? Porque no cumple la premisa inicial: “todo número entero  ...”; es decir, como
...”; es decir, como  no es entero, no se puede aplicar la definición a dicho número.
no es entero, no se puede aplicar la definición a dicho número.
Tenemos también definiciones que no tienen cuantificadores. Veamos algunos ejemplos.
2.2 Definiciones sin cuantificadores

Lo primero que notamos en este libro de geometría, Geometría elemental, de Pogorelov, es que las definiciones no están señaladas como antes; en este caso se encuentran dentro del propio texto y detectarlas está a cargo de quien lee.
 Buscá en el texto las definiciones de rectángulo, rombo y cuadrado
Buscá en el texto las definiciones de rectángulo, rombo y cuadrado
En este caso las tres definiciones planteadas no tienen cuantificadores; simplemente enuncian una propiedad que deben cumplir los objetos para recibir el nombre dado en la definición. En el caso del rectángulo, por ejemplo, sus cuatro ángulos deben ser rectos. También es interesante notar que la definición de cuadrado involucra a la definición de rectángulo, por lo que todo cuadrado es a su vez un rectángulo. Es decir, tenemos que un tipo de objeto puede estar incluido dentro de otro tipo de objeto.
2.3 Definiciones equivalentes
Algunas definiciones pueden darse de maneras diferentes (en algunos casos, ¡muy diferentes!) pero de forma tal que queden definidos exactamente los mismos objetos. En ese caso se habla de definiciones equivalentes. Un ejemplo sencillo es definir a los números pares de la siguiente manera:
Definición. Todo número entero  se dice par si el resto de dividir a se dice par si el resto de dividir a  por por  es cero. es cero. |
Claramente, no es la misma definición que la enunciada anteriormente, ya que esta nueva definición no involucra la existencia de otro número y se refiere a la operación de división entera, en lugar de la multiplicación. Sin embargo, todo número que cumpla con la primera definición cumple con esta nueva definición, y todo número que cumpla con la definición de resto cero cumplirá con la primera. Veamos la demostración:
Si  se puede escribir como
se puede escribir como  , es decir,
, es decir,  , tenemos que:
, tenemos que:
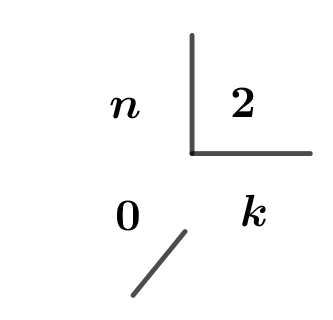
es decir, el resto es cero.
Al revés, si el resto de dividir a  por
por  fuera cero, tenemos que
fuera cero, tenemos que  debe escribirse como producto del divisor por el cociente más el resto (
debe escribirse como producto del divisor por el cociente más el resto ( es el divisor,
es el divisor,  el cociente,
el cociente,  el resto), es decir
el resto), es decir  , o equivalentemente,
, o equivalentemente,  .
.
Por ende, se trata de definiciones equivalentes.
2.4 Definiciones “difíciles”
Existen algunas definiciones para las cuales resulta difícil (a veces, ¡muy difícil!) decidir si un objeto matemático las cumple o no. Veamos la siguiente definición:
Definición. Se llama número irracional a todo número que no puede expresarse como cociente  entre dos números enteros, con entre dos números enteros, con  . . |
Por ejemplo, el número  cumple con esta definición. Para poder ver que dicho número es irracional es necesario demostrar que no existe ninguna fracción
cumple con esta definición. Para poder ver que dicho número es irracional es necesario demostrar que no existe ninguna fracción  que elevada al cuadrado dé como resultado 2. Dejaremos para más adelante esta demostración, que no es inmediata.
que elevada al cuadrado dé como resultado 2. Dejaremos para más adelante esta demostración, que no es inmediata.
El número  , que es la cantidad de veces que un diámetro “cabe” en una circunferencia de dicho diámetro, es irracional. Existen muchas demostraciones de este hecho; todas son sumamente difíciles e involucran conceptos de análisis matemático o de teoría de números. La primera demostración de que
, que es la cantidad de veces que un diámetro “cabe” en una circunferencia de dicho diámetro, es irracional. Existen muchas demostraciones de este hecho; todas son sumamente difíciles e involucran conceptos de análisis matemático o de teoría de números. La primera demostración de que  no es racional fue realizada por el matemático Johann Lambert en 1760.
no es racional fue realizada por el matemático Johann Lambert en 1760.
3. Saber más
Los objetos matemáticos fueron definidos de distintas maneras según las épocas e incluso según los matemáticos que trabajaron con ellos. Veamos dos ejemplos.
3.1 La definición de cuadrado en la historia
Euclides fue un matemático griego de los siglos IV-III A.C. Su obra más conocida, Elementos, contiene la siguiente definición:

¿Son estas las mismas definiciones que las que vimos en la sección 2? No, puesto que para la definición de Euclides un cuadrado no es un rectángulo, en tanto que para la definición del libro Geometría Elemental, sí lo es. ¿Y entonces? ¿Cuál de las dos definiciones de cuadrado es la correcta? No existe una definición correcta; lo que existe es una definición de uso más corriente que la otra. Hoy en día, se asume como definición de uso corriente la que considera que un cuadrado es a la vez rombo y rectángulo. Por ejemplo, en el libro Entre Números III (para la escuela secundaria) encontramos esta definición del cuadrado y demás cuadriláteros:
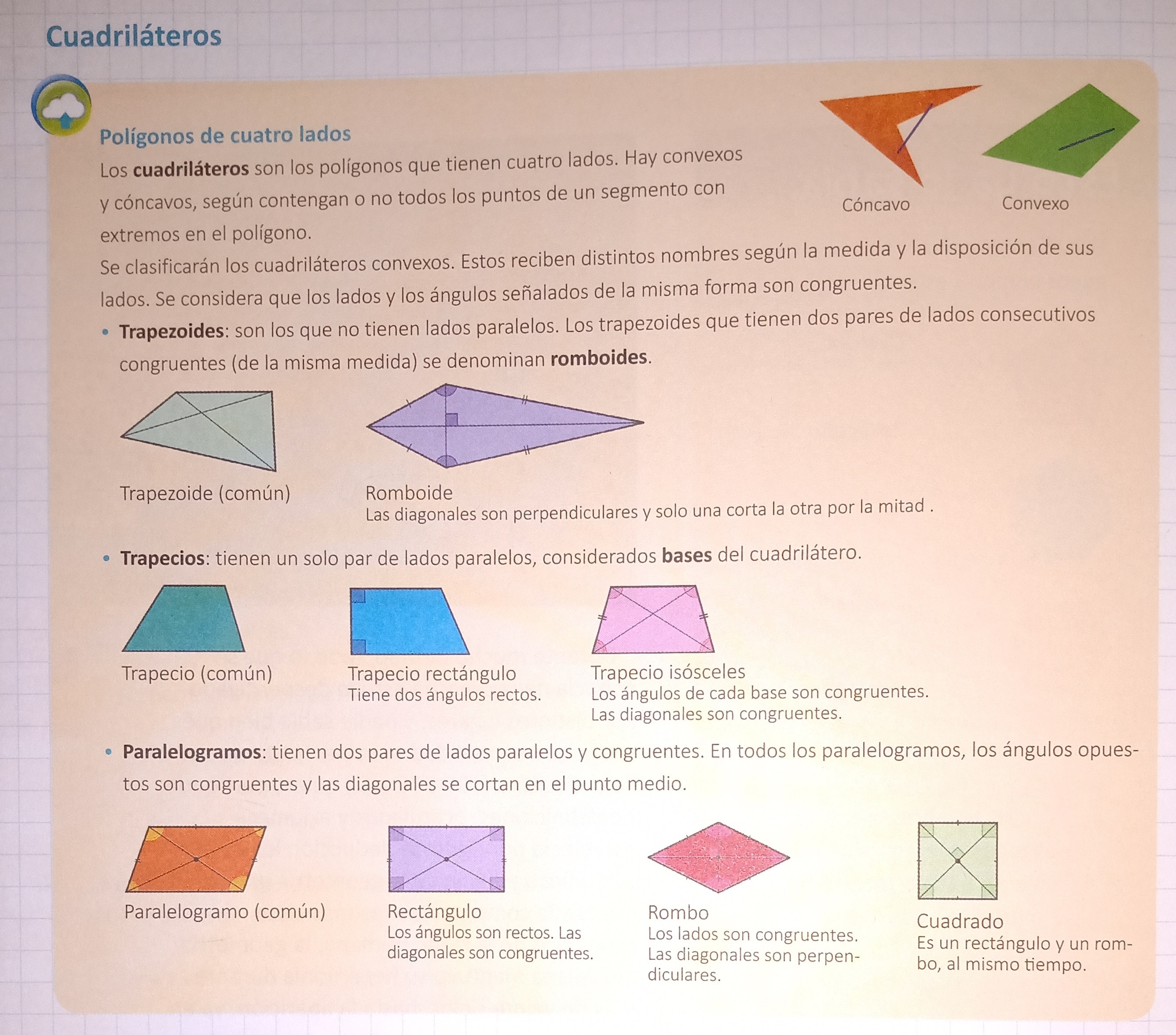
Fuente: Jaller, A. y Pérez, M. (2016).
.
3.2 La definición de función en la historia
Tampoco la idea de función fue la misma a lo largo de la historia de la matemática. Si consultamos el clásico Análisis Matemático I de J. Rey Pastor, Trejo y Pi Calleja, nos encontraremos con lo siguiente:

Vemos aquí que los autores trabajan con una idea diferente de función de la que vimos (y de uso usual): aquí nos hablan de funciones uniformes y multiformes, que pueden tomar diversos valores.
Hoy se acepta como definición de función -de uso frecuente- la que dice que a cada valor del dominio le corresponde una y solo una imagen en el codominio, tal como vimos en el texto anterior, el Cálculo de Piskunov. Sin embargo la definición de función multiforme (o multivariada) resulta fértil en algunos campos de la matemática en los que se sigue utilizando.
Como cierre de esta sección, te proponemos realizar la siguiente autoevaluación:
|
Si no tenés un usuario creado en este campus no podés hacer las autoevaluaciones. Te dejamos las instrucciones para poder realizarlas:
|
4. Bibliografía de consulta
- Euclides (2007). Elementos. Madrid: Gredos.
- Jaller, A. y Pérez, M. (2016). Entre números III. Buenos Aires: Santillana.
- Piskunov, N. (1980). Cálculo diferencial e integral, tomo I. Moscú: Editorial Mir.
- Pogorelov, A. V. (1974). Geometría elemental. Moscú: Editorial Mir.
- Rey Pastor, J.; Pi Calleja, P. y Trejo, C. A. (1952). Análisis Matemático I. Buenos Aires: Kapelusz.