3. LOS TEOREMAS EN MATEMÁTICA - PARTE 1

En las diversas ramas de la ciencia, los nuevos avances se comunican a través de publicaciones o papers. Una publicación puede ser más o menos extensa, de acuerdo a la profundidad y complejidad del tema. En 1966 se dio a conocer una famosa publicación matemática, conocida como por ser la más breve:

La traducción del texto anterior (¡de apenas cinco líneas!) es la siguiente:

(*) Esta fue una de las primeras supercomputadoras de la historia. (https://es.wikipedia.org/wiki/CDC_6600)

¿Qué dice dicha publicación? En 1769 el matemático suizo Leonhard Euler hizo la siguiente conjetura:

Veamos un ejemplo con $n = 3$. Si se quiere obtener $4^3$ como suma de otros cubos, son necesarios al menos $5$ cubos (no lo mostraremos aquí, pero se puede ver agotando las combinaciones entre cubos menores a $4^3$), ya que:

$4^3 = 3^3 + 3^3 + 2^3 + 1^3 + 1^3$

¿Qué es una conjetura? Es una afirmación que se sospecha verdadera, pero de la que aún no se tiene una prueba completa de su validez. Si una conjetura se demuestra verdadera, se la llamará teorema (o lema, o proposición, de acuerdo a su importancia). En cambio, basta un solo contraejemplo, para derribar la conjetura. La publicación de 1966 muestra precisamente un contraejemplo -que Euler no pudo hallar- obtenido mediante una supercomputadora de la época. Allí se muestra que una potencia quinta se puede obtener como suma de cuatro potencias quintas (y la conjetura decía que se debía necesitar por lo menos cinco).

2.1 ¿Qué son los teoremas?

En matemática, un teorema es una proposición sobre la que se ha podido establecer lógicamente su validez a partir de otro conjunto de axiomas o teoremas. De forma “vaga” (ambigua) es un argumento que relaciona el valor de verdad de una afirmación a partir del valor de verdad de otras ya establecidas.

Su estructura semántica interna puede describirse de forma genérica a partir del esquema:

• hipótesis: son los supuestos que se plantean para los objetos matemáticos de los que trata el teorema;

• tesis: es la afirmación que se quiere demostrar;

• demostración: es la secuencia de pasos lógicos que permiten ir de las hipótesis a la tesis. Al final de una demostración suele escribirse algún símbolo que indica la finalización; en muchos textos se utiliza la sigla Q.E.D. que significa (quod erat demonstrandum, traducido como “queda entonces demostrado”).

Este esquema muchas veces no se deja explícito pero es el sustrato de la argumentación lógica.

.

2.2 Algunos teoremas sencillos

Veamos algunos teoremas de la geometría. Un teorema sencillo es el siguiente:

Demostración. Sea un triángulo ABC. Supongamos, sin pérdida de generalidad, que su base AB se opone al ángulo mayor C, de manera que la altura esté contenida dentro del triángulo.

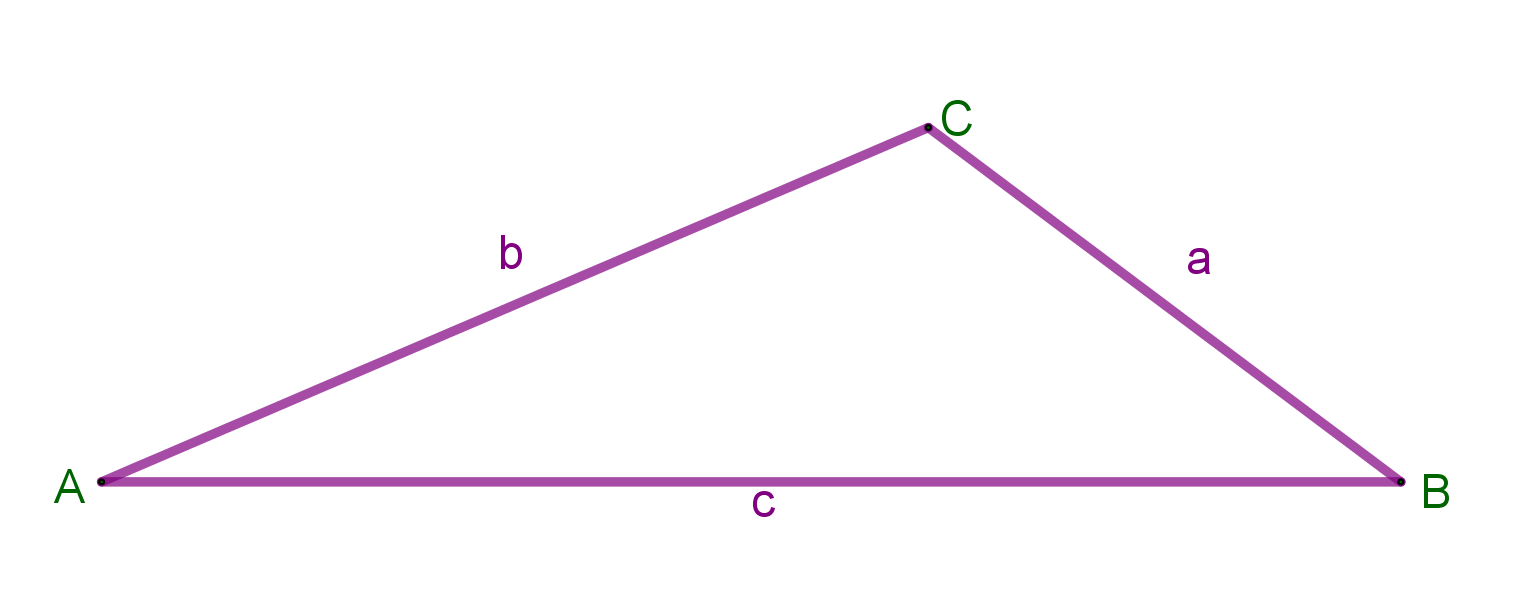
Trácense las rectas paralelas a la altura que pasen por los vértices A y B. Trácese también la recta paralela al lado AB que pase por C. Sean P el punto del lado AB que es pie de la altura correspondiente; sean M y N las intersecciones entre las rectas trazadas como se ve en la figura.

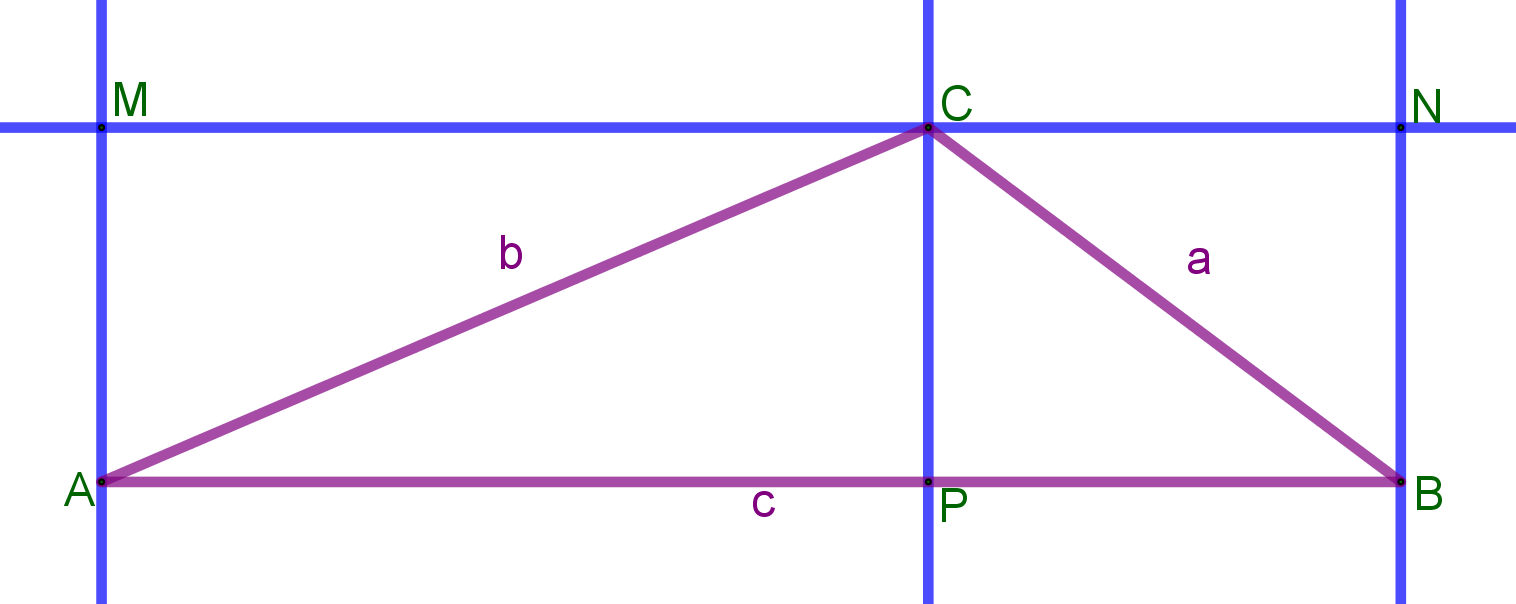
Los triángulos ACP y ACM resultan iguales, por ser mitades del rectángulo AMCP, ya que AC es su diagonal. Los triángulos BCP y BCN resultan iguales, por ser mitades del rectángulo BNCP, ya que BC es su diagonal. Por lo tanto:

Área(AMNB) = Área(ACP) + Área(ACM) + Área(BCP) + Área(BCN) = 2(Área(ACP) + Área(BCP))

Como Área(ACB) = Área(ACP) + Área(BCP), se concluye que

Área(AMNB) = 2Área(ABC)

O equivalentemente: el área del triángulo ABC es la mitad de la del rectángulo AMNB. Q.E.D.

¿Cuál es la hipótesis de este teorema? ¿Cuál es la tesis? La tesis es lo que se afirma al final: es decir, que el área del triángulo es igual a la mitad de la del rectángulo de igual base y altura. Este teorema es un resultado tan general que no es necesaria ninguna hipótesis sobre el triángulo que se analiza (“sea un triángulo ABC”). Al pedir que AB sea el lado mayor, parecería haber una condición (una hipótesis) sobre el triángulo; pero no es así, ya que dado un triángulo ABC podemos cambiar los nombres de sus vértices de modo que AB sea el lado mayor.

Notemos también que el teorema hace uso de algunos resultados auxiliares (que se asumen como “verdades”): la altura respecto del lado mayor está contenida en el triángulo, la diagonal de un rectángulo lo divide en dos triángulos de igual área. Estos resultados podrían demostrarse aparte (son también teoremas) haciendo uso de los axiomas de la geometría.

2.3 Más teoremas

Para seguir profundizando en la idea de teorema, veremos ahora algunos teoremas en otros contextos. En primer lugar veamos un teorema que relaciona el seno y el coseno de ángulos complementarios.

Hipótesis. Sean $\alpha$ y $\beta$ dos ángulos complementarios, es decir, su suma es $\frac{\pi}{2}$ (usaremos radianes para medir ángulos, de modo que $90^{\circ}$ equivale a $\frac{\pi}{2}$).

Tesis. $\text{sen}(\alpha)=\text{cos}(\beta)$

Demostración. Si ninguno de los ángulos $\alpha$ y $\beta$ es nulo, podemos construir el siguiente triángulo:

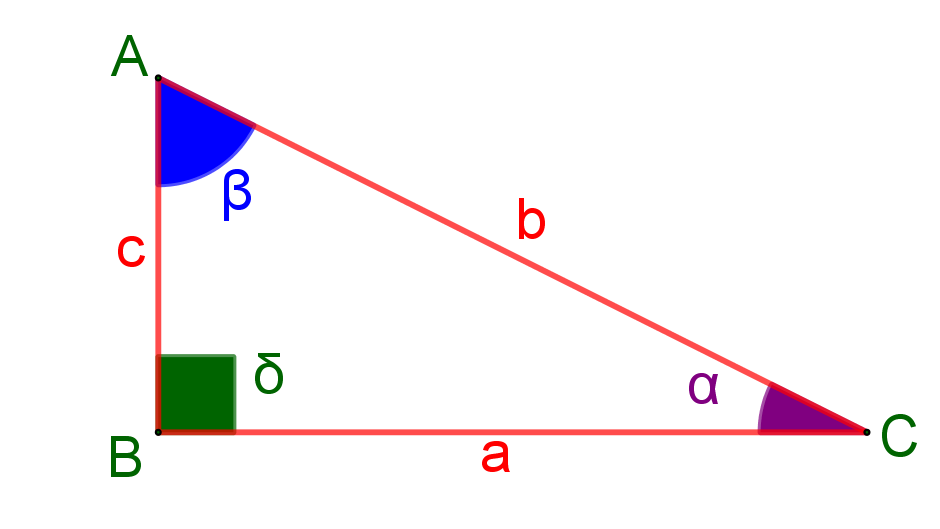
ABC es un triángulo rectángulo: $\delta = \frac{\pi}{2}$

$\alpha + \beta = \frac{\pi}{2}$

En el triángulo rectángulo ABC, se sabe que $\alpha + \beta = \frac{\pi}{2}$.

Como $\text{sen}(\alpha)=\frac{\overline{AB}}{\overline{AC}}$ y $\text{cos}(\beta)=\frac{\overline{AB}}{\overline{AC}}$, luego: $\text{sen}(\alpha)=\text{cos}(\beta)$

Quedan por analizar los casos:

a) $\alpha=0$ y $\beta=\frac{\pi}{2}$

Como $\text{cos}(0)=1$ y $\text{sen}\left(\frac{\pi}{2}\right)=1$, se verifica la igualdad.

b) $\alpha=\frac{\pi}{2}$ y $\beta=0$.

Como $\text{cos}\left(\frac{\pi}{2}\right)=0$ y $\text{sen}(0)=0$, se verifica la igualdad. Q.E.D.

Otro interesante teorema, que se relaciona con la conocida regla de Ruffini, es el teorema del resto para polinomios.

Hipótesis. $P(x)$ es un polinomio de grado mayor o igual a 1 con coeficientes reales y $a \in \mathbb{R}$ en el polinomio $(x - a)$.

Tesis. $r = P(a)$

Demostración. Si realizamos la división entre los polinomios $P(x)$ y $(x - a)$ obtenemos un cociente $C(x)$ y un resto $R(x)$ tales que:

$P(x) = C(x) \cdot (x - a) + R(x)$

Como el grado del resto debe ser menor que el grado del divisor, se concluye que el resto tiene grado 0, pues el divisor tiene grado 1. Los polinomios de grado 0 son constantes, de modo que $R(x) = r$.

Si $(x - a) = 0$, se deduce que $x = a$. Entonces

$P(a) = C(a) \cdot 0 + r$

De aquí se deduce que

$P(a) = r$

Q.E.D.

Hemos presentado aquí los teoremas de modo que queden claras sus hipótesis y tesis. Sin embargo, no todos los libros son tan claros al momento de mencionar las hipótesis, o incluso al enunciar el teorema mismo. Por ejemplo, E. Gentile en su libro Notas de Álgebra, muestra esta demostración de la unicidad del elemento $0$ en los números reales $(\mathbb{R})$.

Notemos que aquí el autor menciona entre paréntesis en la demostración el uso de una hipótesis (que el $0^*$ es elemento neutro y $0^* + \text{a} = \text{a}$; análogamente para $0$).

Un problema interesante es la llamada conjetura de Collatz (también llamada conjetura $(3n+1)$), planteada en 1937. Tomen un número natural cualquiera; si es par divídanlo por $2$, si es impar multiplíquenlo por $3$ y sumen $1$. Repitan el proceso… Por ejemplo, si tomamos $5$, eso nos conduce a:

$5$

$3 \cdot 5 + 1 = 16$    (triplicamos y sumamos 1 porque 5 es impar)

$16 \text{ }:\text{ }2 = 8$    (dividimos por 2 porque 16 es par)

$4$

$2$

$1$

$4$

$2$

$1...$

Vemos que una vez que llegamos al $1$, se inicia un ciclo periódico $(4, 2, 1)$. ¿Y si comenzamos por otro número? La conjetura establece que no importa qué número tomemos como valor inicial, siempre terminaremos en el ciclo $(4, 2, 1)$.

¿Por qué es una conjetura y no un teorema? Porque aún no se ha logrado demostrar su validez. Hasta donde se ha probado (con números muy grandes) se sigue obteniendo el mismo resultado: $(4, 2, 1)$. Pero no alcanza con probar y probar ya que nunca podríamos garantizar la validez para todos los números naturales, que son infinitos. Muchos matemáticos y matemáticas actuales siguen intentando demostrar la conjetura; entre ellos Terrence Tao, quien realizó avances muy recientemente en 2019.

A continuación te ofrecemos:

• El enunciado y estado actual del problema:  https://es.wikipedia.org/wiki/Conjetura_de_Collatz 

• Un video -en inglés- que explica algunos avances sobre la conjetura de Collatz: https://www.youtube.com/watch?v=094y1Z2wpJg 

.

Otra conjetura famosa, aún no demostrada, es la llamada conjetura de Goldbach. El matemático Cristian Goldbach postuló en 1742 que todo número par mayor que 2 puede escribirse como la suma de dos números primos.

Por ejemplo, el número $100 = 3 + 97$; $3$ y $97$ son primos, lo que es un ejemplo de la conjetura. ¿Te animás a encontrar la descomposición como suma de dos primos de $120$? ¿Y de $88$?

En este blog de matemática podés encontrar información acerca de esta conjetura: https://www.gaussianos.com/la-conjetura-de-goldbach/ 

Del mismo modo que la conjetura de Collatz, se ha intentado sin éxito demostrar la conjetura de Goldbach. Pero esta última lleva casi tres siglos resistiéndose. ¿Serán demostradas estas conjeturas alguna vez?

Como cierre de esta sección, te proponemos realizar la siguiente autoevaluación:

• Autoevaluación