4. LOS TEOREMAS EN MATEMÁTICA - PARTE 2

Los antiguos babilonios desarrollaron un sistema de escritura llamada cuneiforme. La siguiente tablilla (correspondiente al período 2000-1600 A.C.) contiene textos matemáticos:

Imagen: British Museum

¿De qué habla esta tablilla? Da un problema de matemática: "He sumado el área y el lado de un cuadrado [y he obtenido] $\frac{3}{4}$". La tablilla además da los pasos para resolver el problema y da la solución: el lado del cuadrado mide $\frac{1}{2}$. Los pasos que muestra la tablilla (que no reproduciremos aquí) son semejantes a los pasos intermedios que obtendríamos al aplicar la fórmula resolvente de cuadráticas a la ecuación $x^2 + x = \frac{3}{4}$. Es decir:

$\frac{-1 + \sqrt{1 + 4 \cdot 1 \cdot \frac{3}{4}}}{2}$

Estamos aquí omitiendo la solución negativa de esta ecuación $-\frac{3}{2}$, puesto que los babilonios no conocían los números negativos.

La tablilla no muestra de dónde se obtiene el procedimiento, sino que simplemente lo enuncia y lo utiliza. ¿Cómo podemos demostrar la validez general de la fórmula resolvente?

Demostración.

$ax^2 + bx + c = 0$

Dividimos por $a$ (recordemos que es distinto de 0):

$x^2 + \frac{b}{a}x + \frac{c}{a} = 0$

Multiplicamos y dividimos por 2 el segundo término:

$x^2 + 2 \cdot \frac{b}{2a}x + \frac{c}{a} = 0$

Sumamos y restamos el cuadrado de $\frac{b}{2a}$, es decir $\frac{b^4}{4a^2}$:

$x^2 + 2 \cdot \frac{b}{2a}x + \frac{b^4}{4a^2} + \frac{c}{a} - \frac{b^4}{4a^2} = 0$

Los tres primeros términos son un cuadrado de binomio, de modo que nos queda:

$\left(x + \frac{b}{2a}\right)^2 + \frac{c}{a} - \frac{b^4}{4a^2} = 0$

$\left(x + \frac{b}{2a}\right)^2 = \frac{b^4}{4a^2} - \frac{c}{a}$

Agrupamos:

$\left(x + \frac{b}{2a}\right)^2 = \frac{b^2 - 4ac}{4a^2}$

Como el miembro de la derecha no es negativo por hipótesis, extraemos la raíz cuadrada. Debemos usar módulo, lo que luego nos conduce a dos opciones (representadas con el símbolo $\pm$).

$\left| x + \frac{b}{2a} \right| = \frac{\sqrt{b^2 - 4ac}}{2a}$

$x + \frac{b}{2a} = \pm \frac{\sqrt{b^2 - 4ac}}{2a}$

Despejando $x$ tenemos finalmente:

$x = -\frac{b}{2a} \pm \frac{\sqrt{b^2 - 4ac}}{2a}$

$x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$

Q.E.D.

Podemos decir que esta demostración es constructiva, ya que la secuencia de pasos permite la construcción en este caso de una fórmula general. Veremos otros tipos de demostraciones en las que aparecerán otras formas de razonamiento.

Hemos visto que la demostración de la validez de la fórmula resolvente de cuadráticas es una demostración constructiva. Otro ejemplo de esto es la fórmula para la suma de los primeros $n$ números naturales:

Antes de demostrar esta proposición, veamos un ejemplo de uso de esta fórmula. Si se quieren sumar los números del 1 al 10 podemos hacer:

$\frac{10 \cdot (10+1)}{2} = 55$

Demostración. Organicemos la suma de los números de 1 hasta n de la siguiente manera:

La primera fila tiene una unidad, la segunda 2, la tercera 3, y así hasta la última, que tiene $n$ unidades. Si duplicamos esta cantidad podemos organizar sus unidades así:

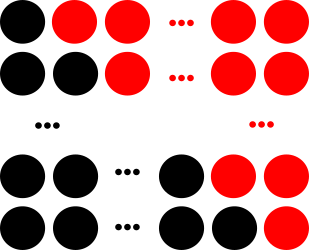
Queda así un rectángulo formado por $n$ filas de $n+1$ unidades; de modo que en total hay $n(n+1)$ unidades. Luego el número $1 + 2 + \dots + n$ tendrá la mitad de este valor, es decir, $\frac{n(n+1)}{2}$. Q.E.D.

.

4.1 Demostraciones por el absurdo

Otro tipo de demostración son las demostraciones por el absurdo.

Fuente: Matemática 4 (De Simone, I. y Turner, M.)

¿Cuál es la idea de una demostración por el absurdo? Se comienza suponiendo que la tesis no se cumple (en este caso, que $\sqrt{2}$ es un número racional). Luego se realizan derivaciones lógicas hasta llegar a un absurdo. De tal modo, no queda otra alternativa que concluir que la premisa inicial (la tesis no se cumple) es falsa.

4.2 Contraejemplos

Algunas demostraciones utilizan la búsqueda de contraejemplos. Un contraejemplo es un ejemplo que da cuenta de la falsedad de una proposición. Por ejemplo:

Demostración. Si suponemos que la igualdad es verdadera, debería cumplirse para cualquier par de números $a$ y $b$. Pero si $a = 3$ y $b = 4$, sucede que $(3+4)^2 = 49 \neq 3^2 + 4^2 = 25$. Es interesante observar que si tomamos $a = 0$ o $b = 0$, la igualdad se verifica; sin embargo, un ejemplo no garantiza la inexistencia de contraejemplos.

Debemos tener en cuenta que los ejemplos de demostraciones que vimos no constituyen una clasificación exhaustiva ni pretenden serlo en la práctica. Mientras que la comunidad matemática acepte una argumentación como válida esta será una demostración. Para complementar esto veamos la siguiente proposición que tiene una interesante demostración.

Demostración. Tomemos el número $\sqrt{2}$; sabemos que este número es irracional. Consideremos el número:

$p = \sqrt{2}^{\sqrt{2}}$

El número $p$ o bien es racional, o bien es irracional. Analicemos cada uno de estos casos:

• Si el número $p$ es racional, la proposición queda demostrada, ya que $a = b = \sqrt{2}$ cumplen lo afirmado en ella.
• Si el número $p$ es irracional, podemos considerar entonces el número $(\sqrt{2}^{\sqrt{2}})^{\sqrt{2}}$. Por propiedades de potencias, usando que $\sqrt{2} \cdot \sqrt{2} = 2$, queda:

$(\sqrt{2}^{\sqrt{2}})^{\sqrt{2}} = \sqrt{2}^{(\sqrt{2} \cdot \sqrt{2})} = \sqrt{2}^2 = 2$

Como $2$ es racional, la proposición queda demostrada tomando en este caso $a = \sqrt{2}, b = \sqrt{2}^{\sqrt{2}}$. Q.E.D.

Lo curioso de esta demostración reside en el hecho de que se considera un número que no se sabe si es racional o no, para luego analizar cada caso por separado, ¡sin saber en ningún momento si el número es racional o no! En cualquiera de los dos casos se logra construir un número que satisface lo pedido. Naturalmente, si se supiera que el número $\sqrt{2}^{\sqrt{2}}$ es racional o no, uno de los dos casos carecería de sentido y su análisis sería innecesario; pero al no saberlo, se torna inevitable el análisis de los dos casos.

Separar en casos de análisis es un método usado en ocasiones para demostrar teoremas. Un conocido caso es el de la demostración del teorema de los cuatro colores, que afirma que todo mapa plano puede colorearse con cuatro colores a lo sumo, de manera que regiones lindantes no posean igual color. Este teorema (conjetura en aquel entonces) fue planteado por Francis Guthrie en 1852 y fue demostrado recién en 1976 por los matemáticos Appel y Haken. El trabajo que realizaron estos matemáticos consistió en “reducir” el problema a 1834 configuraciones diferentes y analizar cada una de ellas mediante un programa de computadora.

Como ejemplo del teorema de cuatro colores, veamos el mapa de la República Argentina (realizado por el Instituto Geográfico Militar), con sus provincias coloreadas aquí con cinco colores.

De acuerdo al teorema podemos colorearlo con cuatro colores a lo sumo. Notemos que las provincias de Tucumán, Santiago del Estero, Catamarca y Salta son todas colindantes, de modo que será imposible colorear con tres colores o menos. El siguiente mapa muestra una posible coloración con cuatro colores:

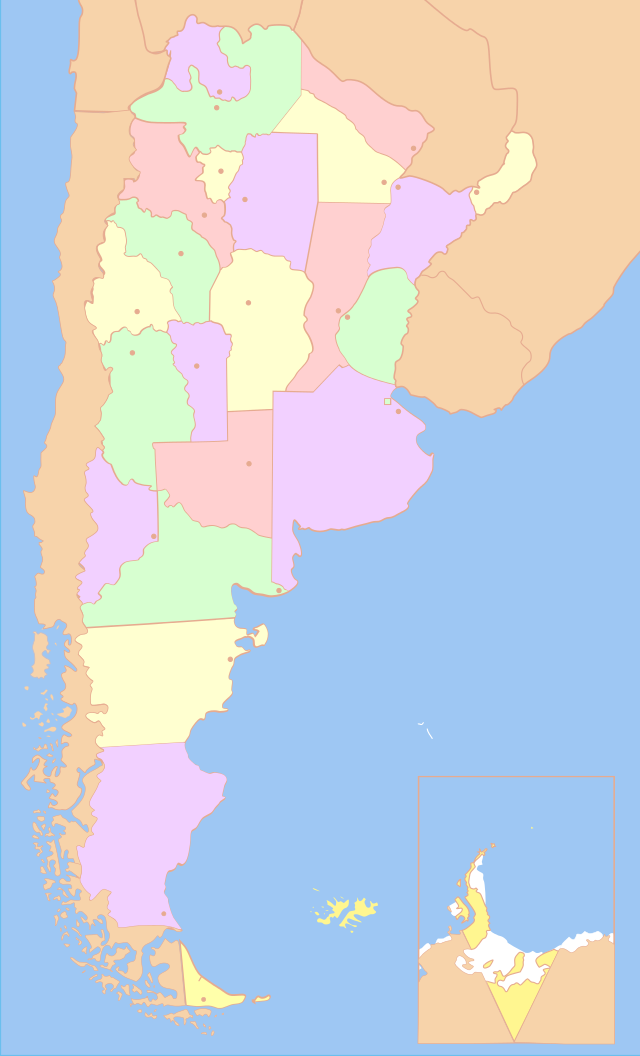
A modo de despedida citaremos este teorema que John Conway incluyó en su libro On numbers and games (1976).

Hacé clic para mirar un libro

Como cierre de esta sección, te proponemos realizar la siguiente autoevaluación:

• Autoevaluación