BLOQUE 2. Movimiento
| Sitio: | Campus Claves Académica |
| Curso: | Física - EnlaceUBA |
| Libro: | BLOQUE 2. Movimiento |
| Imprimido por: | Invitado |
| Día: | lunes, 16 de febrero de 2026, 03:08 |
1. Entrando en tema
Una breve presentación del tema de este bloque: el estudio del movimiento.
Bueno, les propongo que comencemos. Unas palabras sobre el tema que nos ocupa:
"Todo se mueve
nada está quieto
salvo mi corazón.
La serpiente se arrastra
en su lecho de piedra
y la piedra se desliza
al costado del volcán
y el viento
es aire en movimiento
nada está en calma
salvo mi corazón"
Moledo, L., & Olszevicki, N. (2014). Historia de las ideas científicas: de Tales de Mileto a la Máquina de Dios (No. 001 (091)). Planeta.
2. Movimiento
Como primera medida leamos atentamente este ejemplo haciendo clic aquí. En esta historia podemos encontrar un primer concepto importante, el del punto de referencia.
El punto de referencia es el lugar desde donde elegimos analizar el movimiento. Los análisis del movimiento que pueden hacer el tripulante y el pescador de la historia son distintos según sus puntos de referencia. Como existen muchísimos puntos de referencia posibles para cada situación, para que nuestras observaciones puedan ser comunicadas a otros observadores e interpretadas correctamente, debemos definir la posición de un cuerpo empleando un sistema de coordenadas. El sistema de coordenadas nos sirve para poder ubicarnos en el espacio y determinar cambios de posición.
|
¿Qué es un cuerpo en Física? En Física, un cuerpo es conocido también como objeto físico, y se caracteriza por tener masa, peso y volumen. |
3. Coordenadas cartesianas
Las coordenadas son grupos de números que describen una posición, ya sea a lo largo de una línea recta, un plano o el espacio. Para indicar coordenadas se emplean los denominados sistemas cartesianos, que consisten en sistemas de referencia constituidos por ejes.
Existen distintos tipos de sistemas de coordenadas cartesianas. Los sistemas cartesianos nos permiten definir la posición de los objetos. En este que vemos acá
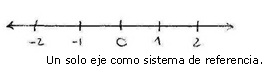
el objeto solamente puede localizarse en algún punto de una línea recta. Es un sistema de una sola dimensión espacial. Este sistema nos va a venir bien cuando tengamos que definir la posición de un tren, por ejemplo, que solamente puede estar en algún punto de una vía ferroviaria.
También existen sistemas que necesitan más dimensiones para definir la posición de un objeto. Vemos acá un ejemplo de ubicación de un punto en un plano (2 dimensiones). El sistema consta de dos ejes perpendiculares (x e y) que se cruzan entre sí en un punto que llamamos origen de coordenadas. Cada eje tiene una escala.
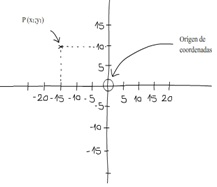
Llamamos coordenadas cartesianas a los valores que definen la posición P.
Veamos un ejemplo de utilización de un sistema de coordenadas haciendo clic aquí.
4. Posición y trayectoria
Como vimos, cada punto de referencia va a originar un sistema de coordenadas cartesianas que permitirá identificar la posición del cuerpo en cada instante. Incluimos aquí la noción del tiempo, dado que el cuerpo puede cambiar su posición. Y así podremos describir el movimiento que estemos analizando.
A esta altura del análisis, ya estamos en condiciones de definir qué entendemos por movimiento de un cuerpo.
Diremos que:
Un cuerpo está en movimiento respecto a un sistema de coordenadas elegido como fijo cuando sus coordenadas varían a medida que transcurre el tiempo.
Por otro lado,
La trayectoria de este cuerpo es la figura formada por la unión con líneas de los distintos puntos que ocupe en el sistema de ejes cartesianos a medida que transcurre el tiempo.
Entonces, a partir del trabajo con sistemas de coordenadas, podemos describir el camino que recorre un cuerpo en su movimiento, concepto que se denomina trayectoria.
| En los próximos contenidos de este BLOQUE aplicaremos los conceptos de "magnitud" y "unidad de medida" desarrollados en el BLOQUE 1. Les recomendamos revisar estos temas antes de continuar la lectura. |
5. Rapidez y velocidad
Ahora que estamos en movimiento describiremos algunos parámetros del mismo. El análisis de la distancia recorrida y el tiempo nos permitirán hablar de rapidez. Si incorporamos la dirección y el sentido al análisis de la rapidez vamos a estar hablando de velocidad.
¿Comenzamos?
RAPIDEZ
Una de las formas de caracterizar un movimiento podría ser conocer la rapidez. La rapidez es una forma de describir al movimiento y relaciona la distancia recorrida con el intervalo de tiempo transcurrido. A partir de este concepto, analicemos el siguiente ejemplo: Un barco que viaja de Buenos Aires a Colonia (el mismo del ejemplo que vieron en 2.Movimiento). De este ejemplo, podemos extraer dos formas de entender la rapidez: la rapidez media y la rapidez instantánea.
La rapidez media nos da información general sobre un determinado movimiento. En el caso del barco, corresponde a la relación entre la distancia total recorrida durante el viaje y el tiempo total del viaje. Se calcula dividiendo la distancia total por el tiempo total del viaje. El valor obtenido es la rapidez media y nos habla del viaje en general. Sin embargo, no sabemos nada sobre las particularidades del viaje.
Otro ejemplo: si realizamos un viaje desde la Capital Federal hasta Mar del Plata y salimos a las 10 de la mañana y llegamos a las 20 habremos recorrido 400 km en 10 horas, la rapidez media sería:
| rapidez media=distancia/tiempo |
rapidez media= 400 km/ 10 h
rapidez media= 40 km/h
En el cálculo de la rapidez media no importa si paramos a cargar nafta o a tomar un café.
Observen que las unidades de rapidez resultan de la relación distancia/tiempo. La distancia la medimos con unidades de longitud (km, m) y el tiempo tiene sus propias unidades de medida (h, s). Las unidades usadas para expresar valores de rapidez son combinadas: km/h ó m/s.
Volvamos al ejemplo del barco (utilizaremos este ejemplo del barco para evaluar todas las características del movimiento). Si miráramos el “velocímetro” del barco tendríamos acceso a esta información sobre los detalles del viaje.
Supongamos que el barco realizó el viaje con una rapidez media de 16,7 km/h, pero también sabemos que en el primer tramo del viaje el barco iba a 25 km/h. Esta rapidez que corresponde a un momento particular del viaje se llama rapidez instantánea. En cualquier momento del primer tramo del viaje, la rapidez instantánea del barco fue de 25 km/h.
En el ejemplo del viaje a Mar del Plata, la rapidez instantánea a la altura de la autopista Buenos Aires- La Plata probablemente fuera 90 km/h y mientras se carga nafta de 0 km/h (el auto está quieto, está en reposo). En cambio, la rapidez media fue la calculada anteriormente considerando la distancia total recorrida y el tiempo total de viaje.
En el gráfico de distancia recorrida en función del tiempo, cada punto del gráfico indica qué distancia ha sido recorrida por el cuerpo en movimiento (llamado móvil) al tiempo correspondiente. Fíjense el siguiente gráfico del ejemplo del barco:
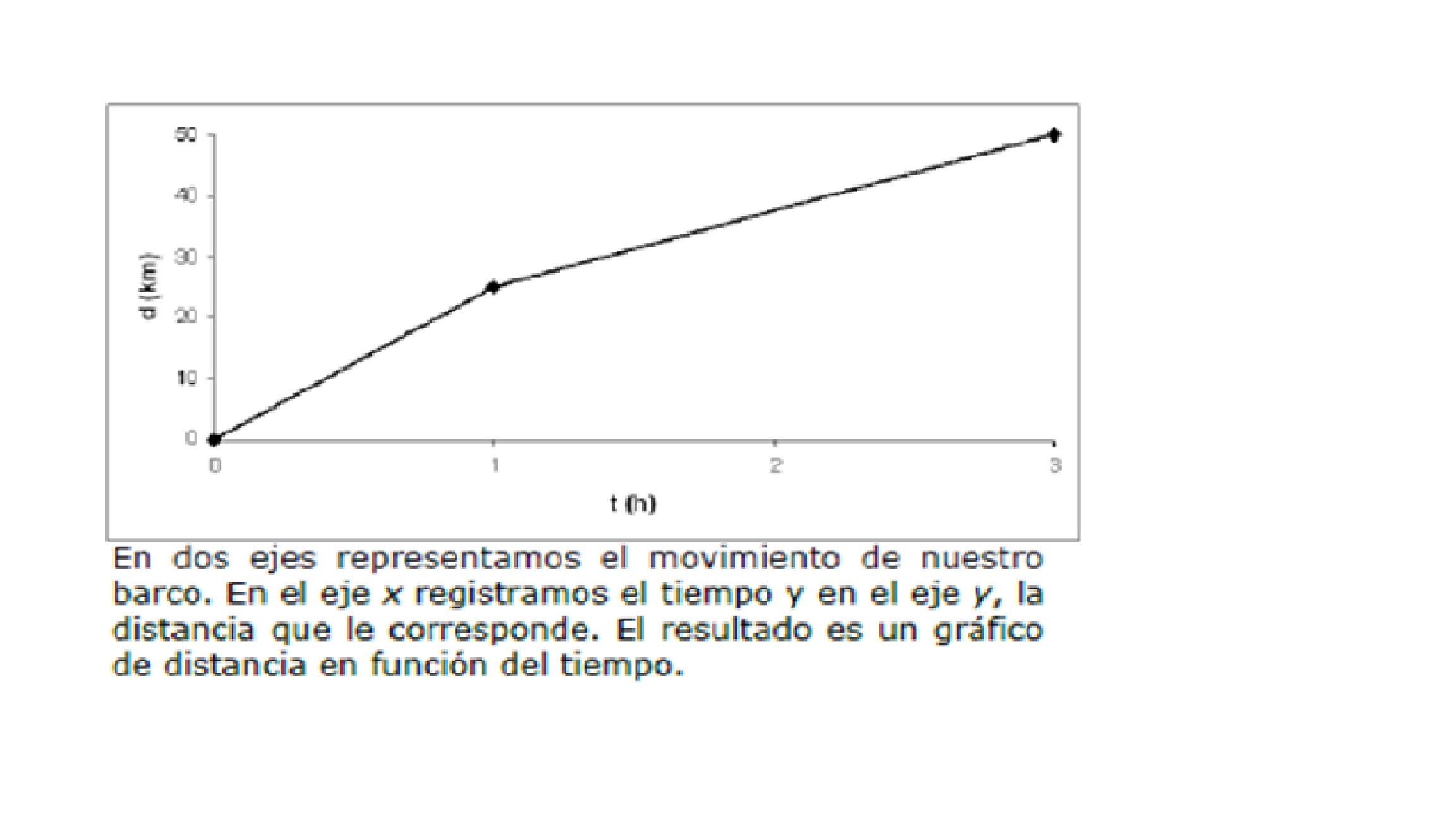
¿Se acuerdan que pasada 1 hora el barco había recorrido 25 km? ¿Dónde está el punto correspondiente? ¿Lo pueden ubicar en el gráfico?
El gráfico representa una función lineal en cada tramo y la pendiente (cuán inclinada es la recta) representa la relación entre la distancia recorrida y el tiempo transcurrido, es decir, la rapidez o velocidad.
VELOCIDAD
Ahora, ¿cuál es la diferencia entre rapidez y velocidad?
Para esto necesitamos introducir los conceptos de magnitudes escalares y vectoriales.
| Una magnitud escalar se define completamente con un valor numérico y una unidad correspondiente. La masa, la temperatura, las longitudes, el volumen son todas magnitudes escalares. Si decimos 20 kg, 10 °C, 50 metros ó 25 cm3 ya alcanza para entender cuánto de estas magnitudes tenemos. Una magnitud vectorial, además de tener un valor numérico y una unidad, tiene una orientación espacial, es decir, tiene dirección y sentido. Los vectores se representan en un esquema con flechas. ¿Recuerdan qué es un vector? Click aquí. |
La rapidez es una magnitud escalar porque se refiere a un valor independientemente de la dirección y sentido del movimiento. La velocidad es una magnitud vectorial: además del valor de la rapidez, también incluye a la dirección y al sentido del movimiento.
Si miran el siguiente esquema, los cuatro coches en movimiento tienen la misma rapidez (50 km/h) pero sus velocidades son distintas porque comparando la dirección de los dos coches en el dibujo de abajo, o el sentido de ambos en el dibujo de arriba, son distintos. No es que las velocidades sean distintas porque una sea mayor o menor que la otra, en este caso son iguales en valor numérico (50 km/h). Son distintas porque difieren en la orientación espacial del movimiento (los coches van “para lados distintos”).
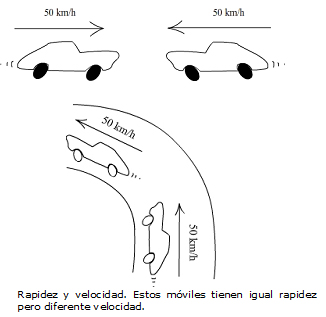
6. Aceleración
Con los conceptos que teníamos hasta ahora, podíamos definir la posición de un cuerpo, analizar su trayectoria y describir a qué velocidad o rapidez ocurría ese movimiento. Con el concepto de aceleración, agregamos la posibilidad de describir cambios en la velocidad o rapidez.
La aceleración es una magnitud física que nos indica la relación entre un cambio en la velocidad de un cuerpo y el tiempo durante el cual ese cambio tuvo lugar. Nos dice “qué tan rápido cambia la velocidad”. Noten que hablamos de cambios y no de aumentos solamente. Esta es una diferencia importante entre el uso físico de aceleración y el uso común de la palabra: también incluye a la desaceleración (lo que llamamos frenado). En Física, cualquier cambio en la velocidad, ya sea aumento o disminución, implica una aceleración, en el primer caso positiva y en el segundo negativa.
| aceleración=variación de rapidez o velocidad / tiempo transcurrido |
Las unidades de aceleración también son compuestas como las de la rapidez y la velocidad. En este caso, en el numerador tenemos unidades de rapidez/velocidad y en el denominador tenemos unidades de tiempo. Por ejemplo, km/h / h ó m/s / s. Las unidades de tiempo están repetidas (en la unidad de rapidez/velocidad y en la unidad de tiempo propiamente dicha). Por lo tanto, se combinan y quedan como unidades de tiempo al cuadrado. Entonces: km/h / h = km/h2 y m/s / s = m/s2.
Trabajemos un poco con los siguientes gráficos. Para ello primero pensemos en el ejemplo del barco que venimos trabajando, ¿en qué momento tendría que haber aceleración?
El barco tuvo que haber acelerado en 3 momentos distintos: cuando el barco partió del puerto, cuando cambió la velocidad a la hora y cuando llegó a destino.
¿Pueden identificar los cambios de velocidad en el gráfico de velocidad en función del tiempo?:
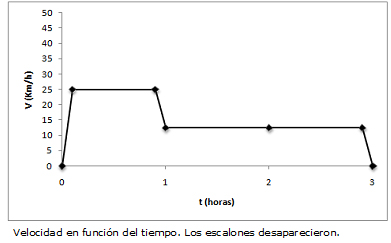
En este caso las rectas horizontales corresponden a los tiempos del recorrido del barco en donde no hubo cambios de velocidad y que por lo tanto la aceleración fue cero. En cambio, las rectas que tienen pendiente distinta de cero a tiempos cero, uno y tres horas corresponden a los momentos de aceleración. ¿Ven que la velocidad cambia en función del tiempo?
También lo podemos ver con el gráfico de abajo en el que se representa la aceleración en función del tiempo ¿en qué momentos la aceleración es distinta de cero? ¿qué significa para la velocidad que la aceleración sea distinta de cero? Significa que la velocidad está variando (aceleración es variación de velocidad en el tiempo).
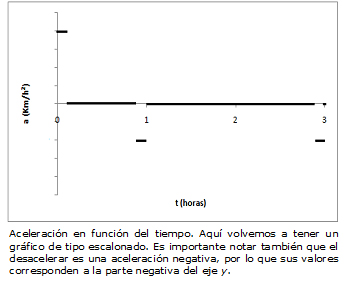
Las líneas horizontales en el valor de aceleración cero, corresponden a momentos del recorrido del barco en los que este no tuvo aceleración, o sea que viajó a velocidad constante.
| Para comenzar a practicar un poco, les proponemos ahora que intenten resolver el siguiente ejercicio: para acceder, hagan click acá. Al finalizar este bloque, encontrarán la respuesta en 9.¿Practicamos? para que puedan autoevaluarse. |
7. Movimientos rectilíneos
Recordemos por un momento el ejemplo del barco (que iba del puerto de Buenos Aires al de Colonia) que tanto hemos utilizado en este bloque. A lo largo de su trayectoria podemos identificar momentos donde la velocidad de la embarcación se mantenía constante (no hay aceleración) y momentos en los que sí variaba la velocidad (hay aceleración).
Un cuerpo que está en movimiento puede moverse con velocidad constante o con velocidad variable. Como tal, podemos describir dos tipos de movimiento:
- Un cuerpo que posea velocidad constante, de modo que recorra distancias iguales en intervalos de tiempo iguales y describa una trayectoria rectilínea, tendrá un movimiento rectilíneo uniforme (en siglas MRU).
-Un cuerpo que tenga aceleración constante distinta de cero y una trayectoria rectilínea, tendrá un movimiento rectilíneo uniformemente variado (en siglas MRUV).
Estudiemos cada uno en particular.
7.1. MRU (Movimiento Rectilíneo Uniforme)
Si el cuerpo recorre distancias iguales en intervalos de tiempo iguales y describe una trayectoria rectilínea, su movimiento se conoce como movimiento rectilíneo uniforme (MRU).
Cuando se habla de distancias recorridas en intervalos de tiempo definidos y de trayectorias (dirección y sentido), estamos hablando de velocidad. Es decir que cuando mencionamos MRU lo debemos asociar con velocidad constante. Recordemos que decir que la velocidad es constante significa que no hay una aceleración.
Por su definición, velocidad constante nos indica que en un intervalo de tiempo definido la distancia recorrida es siempre la misma. Pongamos un ejemplo. Un auto que se traslada a 55 km/h con velocidad constante, cada hora de recorrido va a recorrer 55 km. Entonces un auto que se dirige a Mar del Plata con MRU, a la hora va a haber recorrido 55 km, a las dos horas 110 km, a las 3 horas 165 km y así sucesivamente. Esto lo podemos graficar de la siguiente manera:
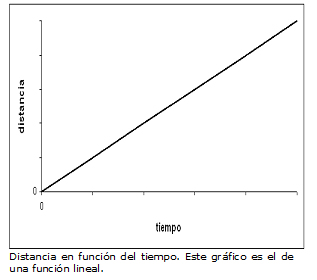
En un gráfico de distancia en función del tiempo, en MRU la pendiente del gráfico representa la velocidad del móvil. Noten que la pendiente de una recta es constante, es una línea recta.
Si la velocidad es constante, entonces el gráfico de velocidad en función del tiempo se ve así:
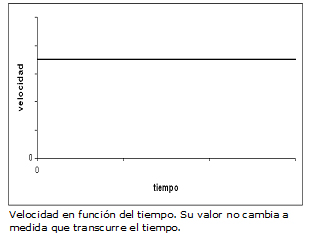
7.2. MRUV (Movimiento Rectilíneo Uniformemente Variado
Un cuerpo que tenga aceleración constante distinta de cero y una trayectoria rectilínea tendrá un movimiento rectilíneo uniformemente variado o MRUV.
¿Qué significa que la aceleración sea constante y distinta de cero?
Significa que, en un intervalo de tiempo definido, la variación de la velocidad va a ser siempre igual y un número distinto de cero. Por ejemplo, si vamos en auto a Mar del Plata describiendo una trayectoria rectilínea y cada 10 minutos aumentamos 10km/h la velocidad. Si el viaje empezara a 50 km/h, a los 10 minutos la velocidad sería 60 km/h. A los 10 minutos siguientes la velocidad sería 70 km/h. A los 10 minutos siguientes la velocidad sería 80 km/h y así sucesivamente. La aceleración en este ejemplo es siempre igual porque lo que varía la velocidad por unidad de tiempo es siempre igual (constante). Ahora, lo que sí cambia es la velocidad. La velocidad en este ejemplo es siempre distinta y esta es la principal diferencia que tiene el MRUV con el MRU.
Dado que la velocidad varía de forma constante con el tiempo, el gráfico de velocidad en función del tiempo en el caso del MRUV se ve así:
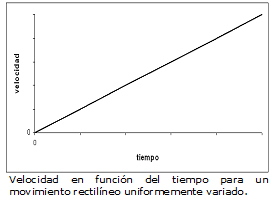
La pendiente del gráfico de velocidad en función del tiempo es la aceleración! Acuérdense que para el MRU como la velocidad del cuerpo es constante, el gráfico de velocidad en función del tiempo se veía como una recta horizontal sin pendiente. En ese caso, la aceleración era cero.
Volvamos al MRUV: que la velocidad siempre varíe igual (como en el ejemplo, donde aumenta 10 km/h cada 10 minutos) significa dos cosas. Una es que la aceleración es siempre la misma y la otra es que a medida que pasa el tiempo recorro más distancia por unidad de tiempo.
En los primeros 10 minutos el auto recorría 50 km cada hora pero en los terceros 10 minutos recorría 80 km por hora. Esta es la otra diferencia con el MRU donde el gráfico de distancia recorrida en función del tiempo era lineal. En MRUV el gráfico de distancia recorrida en función del tiempo toma esta forma:
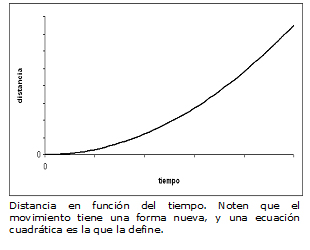
Pueden ver una comparación de los gráficos de MRU y MRUV haciendo click aquí.
7.3. Caída libre
Veamos ahora un ejemplo de movimiento rectilíneo con aceleración constante (MRUV): la caída libre.
¿Cómo caen los objetos? 
¿Qué pasa cuando dejamos caer un mismo objeto desde dos alturas diferentes? Una piedra que cae desde el balcón del quinto piso llegaría a la calle con mayor velocidad que si cayera desde el primer piso.
¿Qué pasa cuando dejamos caer dos objetos de igual masa pero distinta forma desde la misma altura? Una hoja de papel abierta y una hoja idéntica pero hecha un bollo compacto: la hoja de papel en bollo llegará más rápidamente al suelo. ¿Será que el aire genera mayor resistencia a la caída del papel abierto?
Entonces comparemos ahora dos objetos de igual forma pero diferente masa que caen desde la misma altura. Por ejemplo la piedra y el bollo de papel. En este caso la resistencia del aire sería semejante para ambos objetos. ¡Nos sorprendería observar que llegan al piso casi al mismo tiempo!
Galileo Galilei, en el siglo XVII, realizó experimentos de este tipo arrojando pesas desde lo alto de la Torre de Pisa, en los que registraba el tiempo que tardaban en llegar al suelo. Esto le permitió afirmar que la velocidad de los objetos que dejamos caer no depende de su masa. Sus adversarios cuestionaban esta afirmación preguntando por qué una pluma no llega al suelo al mismo tiempo que la piedra. Es que Galileo se dio cuenta que era la forma lo que hacía la diferencia, y no la masa de los objetos (como vimos recién con la hoja abierta y en forma de bollo), ya que de la forma dependerá el rozamiento que ejerce el aire en la caída del objeto.
| Estos experimentos constituyen situaciones reales, pero para entenderlos mejor muchas veces se busca pensar los fenómenos reales sin la influencia de algunas variables. En este caso Galileo trató de eliminar el efecto del rozamiento del aire en la caída, buscando comparar objetos con igual forma. A estas situaciones donde buscamos no considerar ciertas variables las llamamos situaciones ideales. Esto nos ayuda a sacar conclusiones para el sistema ideal que pueden ser válidas en aproximación para un sistema real. |
Y así Galileo concluyó que el desplazamiento de los objetos era proporcional al cuadrado del tiempo que se mantenían en movimiento.
Entonces, llamamos caída libre al movimiento de un cuerpo bajo la acción exclusiva de la gravedad. Este es un movimiento acelerado (con aceleración constante), vertical y hacia el centro de la Tierra. ¡Y las ecuaciones que lo describen son las que estudiamos para MRUV!
Actualmente disponemos de dispositivos para generar vacío, de modo que podemos suprimir el efecto del rozamiento del aire en el experimento. Si dejáramos caer la hoja de papel abierta y la piedra en estas condiciones de vacío, veríamos que ambas caen al mismo tiempo.
Dos cuerpos cualesquiera que se dejen caer de forma simultánea y desde la misma altura en el vacío, caerán siempre juntos con igual velocidad y tardarán el mismo tiempo en llegar al suelo.
Y así podemos afirmar que en el vacío todos los cuerpos caen con la misma aceleración. La aceleración con la que un cuerpo cae se denomina aceleración de la gravedad.
En las ecuaciones de MRUV representamos la aceleración con la letra a. Cuando nos referimos en particular a la aceleración de la gravedad usamos la letra g.
El valor de g depende de la constante de gravitación universal (G), de la masa de nuestro planeta (M) y del cuadrado de la distancia que hay desde su centro hasta el objeto (d2):
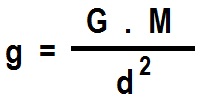
¿Se dan cuenta que en esta fórmula no aparece la masa del objeto? La aceleración de la gravedad es independiente de la masa del objeto que cae. Para nuestros cálculos en ecuaciones de MRUV, consideraremos que su valor aproximado en la Tierra es:
Cualquier objeto que se mueva bajo la influencia de la gravedad caerá libremente una vez liberado del impulso original, con una aceleración dirigida hacia la Tierra. Así un objeto lanzado hacia arriba también caerá finalmente hacia abajo en caída libre.
8. Para saber más ...
- Les proponemos ver un video muy cortito, que nos servirá para seguir pensando el concepto de punto de referencia. ¿Dónde estamos ubicados en el Universo?
Sinopsis: Seguro que sabes la dirección de tu casa, pero… ¿Sabes la dirección completa de tu planeta? ¿Conoces dónde está metida la Tierra? Descubre cómo se organiza el Universo en este vídeo.
- Y además, este otro es un enlace interesante para mirar y reflexionar sobre el movimiento de rotación de la tierra:
Sinopsis: ¿Por qué gira la Tierra? Cuando una pelota sale disparada de una calesita, ¿cae en curva, como parece, o cae en línea recta? ¿Cómo se puede manipular la velocidad en la rotación? En resumen, ¿por qué el movimiento giratorio es tan especial? Brian Jones detalla la vertiginosa amplia gama de formas en que el movimiento de rotación afecta nuestras vidas.
Nota: no se preocupen por las ecuaciones que se muestran en el video, son conceptos que no llegaremos a ver en profundidad en nuestros curso de Física, pero que son fundamentales para explicar de manera completa estos fenómenos.
9. ¿Practicamos?
- Bajo el título 6.Aceleración, para comenzar a practicar un poco, les propusimos que intentaran resolver el siguiente ejercicio: para acceder, hagan clic acá. Si todavía no lo hicieron pueden resolverlo ahora. Y aquí les ofrecemos las respuestas para que puedan autoevaluarse.
- Veamos ahora un ejemplo de cómo interpretar un gráfico. Haciendo clic acá pueden descargar el archivo.
- Además, les proponemos usar un simulador computacional sobre caída libre. ¿Qué es esto? Bueno, básicamente un programa computacional como cualquier otro pero que, en este caso, realiza cuentas (usando ecuaciones físicas del movimiento, que están previamente cargadas en el programa) para decirnos en qué momento caerán unas esferas de una hipotética Torre de Pisa virtual. ¿Por qué desde la Torre de Pisa? Bueno, porque, como vimos, en los años 1600, Galileo Galilei comenzó sus observaciones soltando dos objetos al mismo tiempo desde lo alto de la torre de Pisa y midiendo el tiempo que tardaban en llegar al suelo. Utilizó diferentes materiales y pesos para poder establecer comparaciones. Por supuesto, para simular una caída libre de dos objetos, tenemos algunas variables a tener en cuenta: la densidad del aire, las masas de las esferas cayendo, las alturas. Para reproducir su experimento, seleccionen la densidad del aire en 1.2 Kg/m3 y la altura en 130 m. Acá les dejamos el enlace al simulador: clic acá.
10. Autoevaluación
Aquí dejamos el cuestionario de autoevaluación para que puedas ver cuánto aprendiste.
|
Si no tenés un usuario creado en este campus no podés hacer las autoevaluaciones. Te dejamos las instrucciones para poder realizarlas:
|