Física - EnlaceUBA

Hasta el momento hemos caracterizado los elementos esenciales de lo que llamaremos energía mecánica, que son: la energía cinética y la energía potencial. La energía mecánica (Em) de un sistema determinado es el conjunto de energía asociada a su posición relativa (energía potencial) y/o a su movimiento (energía cinética). Pudiendo expresarse como:
                                                  Em = Ec + Ep

Ahora, que definimos de qué depende la Energía Mecánica, pensemos en la siguiente pregunta:

¿Existe la conservación de la energía en los sistemas que estudiamos? 

¿Qué significa que la energía se conserve? Bueno, significa que la energía inicial del sistema, es la misma que la energía final. Desde ya, adelanto que esto no ocurre en la mayoría de los sistemas. En general, la energía NO se conserva. 

Vamos el siguiente ejemplo: 
Pensemos en el carro de una montaña rusa que ha quedado detenido en la punta más alta del circuito.

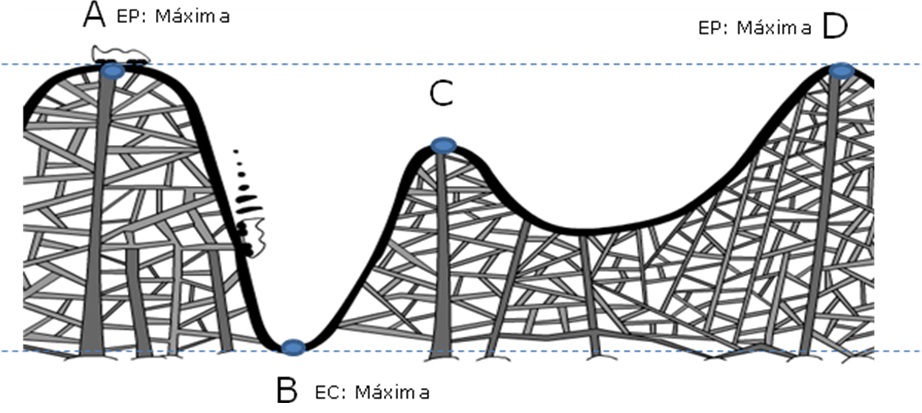
En este ejemplo, un carrito va transformando alternativamente su energía potencial gravitatoria en energía cinética (en los descensos) y la energía cinética en energía potencial gravitatoria (en los ascensos). Fíjense que es posible utilizar la energía potencial gravitatoria acumulada en este sistema para que ocurra un trabajo mecánico y que el carrito se mueva por el tramo descendente de la montaña rusa (de A a B) mientras va ganando energía cinética. Por otro lado, también es posible aprovechar la energía cinética que transporta el carrito para realizar con este “envión” un trabajo mecánico, hacerlo subir por el tramo ascendente (de B a C) y hacerlo ganar energía potencial gravitatoria.

Las energías potencial gravitatoria y cinética se pueden transformar una en otra. El proceso en el cual ocurre esta transformación es un trabajo mecánico. Ambas formas de energía están incluidas en el concepto de energía mecánica, que justamente es la suma de las energías potencial gravitatoria y cinética.

Si se trata de un sistema ideal, no se pierde energía mecánica, de manera que aunque ocurran estas transformaciones el total de energía se mantiene constante. Los sistemas ideales son eso, ideales, es decir, teóricos, que sirven para estudiar distintos fenómenos, pero representan situaciones reales.

En los sistemas reales esto no se cumple porque existe el rozamiento. Cuando un cuerpo se mueve, roza con distintas superficies y con el aire, y el trabajo que  realizan las fuerzas de rozamiento, cuyo sentido es en contra del movimiento, hace que la energía mecánica del cuerpo disminuya.  Esa energía se transfiere al ambiente en forma de calor. De esta manera, cuando el carrito recorre el primer tramo descendente de la montaña rusa (de A a B) una parte de su energía potencial gravitatoria se transforma en energía cinética y la otra parte se pierde debido al trabajo realizado por el rozamiento (W_roz). Por este trabajo del rozamiento, parte de la energía mecánica del sistema se pierde como calor. Cuando el carrito recorre el tramo ascendente de la montaña rusa (de B a C) una parte de la energía cinética se transforma en energía potencial gravitatoria y la otra parte se pierde también en el trabajo por el rozamiento.

Se dice que las fuerzas de rozamiento son no conservativas, ya que en un sistema real, la energía invertida en vencer la acción de las fuerzas de rozamiento representa la diferencia entre  la energía mecánica inicial y la energía mecánica final. 

En el BLOQUE 2 y en el BLOQUE 3 mencionamos las diferencias entre las situaciones ideales y las situaciones reales.

En la Sección 8. ¿Practicamos? encontrarán un simulador computacional para experimentar sobre este tema. También pueden acceder desde acá. Primero, hagan click en ¨friction¨, para experimentar el simulador con rozamiento.