Física - EnlaceUBA

Ahora que estamos en movimiento describiremos algunos parámetros del mismo. El análisis de la distancia recorrida y el tiempo nos permitirán hablar de rapidez. Si incorporamos la dirección y el sentido al análisis de la rapidez vamos a estar hablando de velocidad. 

¿Comenzamos?

RAPIDEZ

Una de las formas de caracterizar un movimiento podría ser conocer la rapidez. La rapidez es una forma de describir al movimiento y relaciona la distancia recorrida con el intervalo de tiempo transcurrido. A partir de este concepto, analicemos el siguiente ejemplo: Un barco que viaja de Buenos Aires a Colonia (el mismo del ejemplo que vieron en 2.Movimiento). De este ejemplo, podemos extraer dos formas de entender la rapidez: la rapidez media y la rapidez instantánea.

La rapidez media nos da información general sobre un determinado movimiento. En el caso del barco, corresponde a la relación entre la distancia total recorrida durante el viaje y el tiempo total del viaje. Se calcula dividiendo la distancia total por el tiempo total del viaje. El valor obtenido es la rapidez media y nos habla del viaje en general. Sin embargo, no sabemos nada sobre las particularidades del viaje.

Otro ejemplo: si realizamos un viaje desde la Capital Federal hasta Mar del Plata y salimos a las 10 de la mañana y llegamos a las 20 habremos recorrido 400 km en 10 horas, la rapidez media sería:

rapidez media=distancia/tiempo

rapidez media= 400 km/ 10 h  

rapidez media= 40 km/h 

En el cálculo de la rapidez media no importa si paramos a cargar nafta o a tomar un café.

Observen que las unidades de rapidez resultan de la relación distancia/tiempo. La distancia la medimos con unidades de longitud (km, m) y el tiempo tiene sus propias unidades de medida (h, s). Las unidades usadas para expresar valores de rapidez son combinadas: km/h ó m/s.

Volvamos al ejemplo del barco (utilizaremos este ejemplo del barco para evaluar todas las características del movimiento). Si miráramos el “velocímetro” del barco tendríamos acceso a esta información sobre los detalles del viaje.

Supongamos que el barco realizó el viaje con una rapidez media de 16,7 km/h, pero también sabemos que en el primer tramo del viaje el barco iba a 25 km/h. Esta rapidez que corresponde a un momento particular del viaje se llama rapidez instantánea. En cualquier momento del primer tramo del viaje, la rapidez instantánea del barco fue de 25 km/h.

En el ejemplo del viaje a Mar del Plata, la rapidez instantánea a la altura de la autopista Buenos Aires- La Plata probablemente fuera 90 km/h y mientras se carga nafta de 0 km/h (el auto está quieto, está en reposo). En cambio, la rapidez media fue la calculada anteriormente considerando la distancia total recorrida y el tiempo total de viaje.

En el gráfico de distancia recorrida en función del tiempo, cada punto del gráfico indica qué distancia ha sido recorrida por el cuerpo en movimiento (llamado móvil) al tiempo correspondiente. Fíjense el siguiente gráfico del ejemplo del barco:

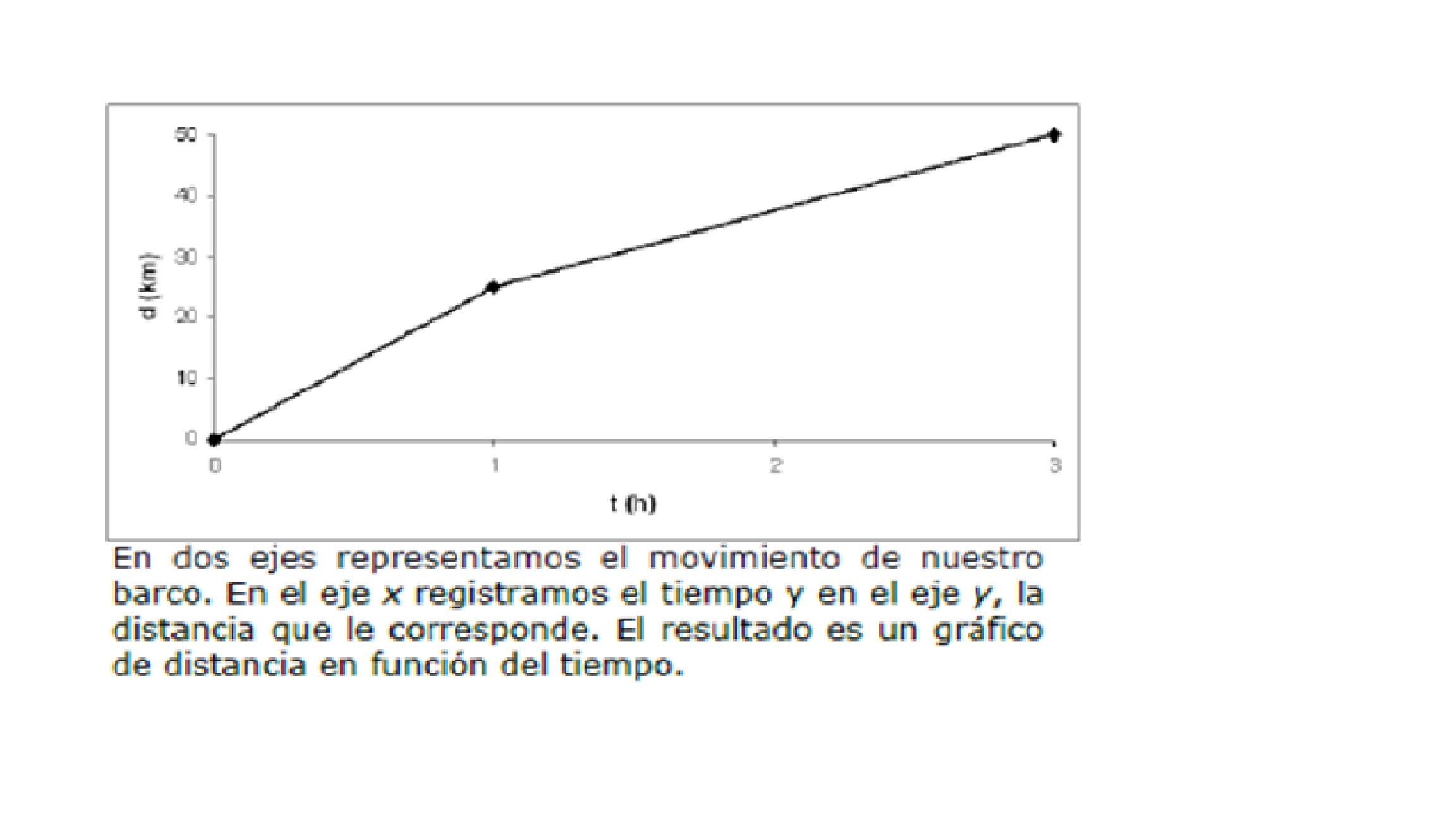
¿Se acuerdan que pasada 1 hora el barco había recorrido 25 km? ¿Dónde está el punto correspondiente? ¿Lo pueden ubicar en el gráfico?

El gráfico representa una función lineal en cada tramo y la pendiente (cuán inclinada es la recta) representa la relación entre la distancia recorrida y el tiempo transcurrido, es decir, la rapidez o velocidad.

VELOCIDAD

Ahora, ¿cuál es la diferencia entre rapidez y velocidad?

Para esto necesitamos introducir los conceptos de magnitudes escalares y vectoriales.

Una magnitud escalar se define completamente con un valor numérico y una unidad correspondiente. La masa, la temperatura, las longitudes, el volumen son todas magnitudes escalares. Si decimos 20 kg, 10 °C, 50 metros ó 25 cm3 ya alcanza para entender cuánto de estas magnitudes tenemos. Una magnitud vectorial, además de tener un valor numérico y una unidad, tiene una orientación espacial, es decir, tiene dirección y sentido. Los vectores se representan en un esquema con flechas. ¿Recuerdan qué es un vector? Click aquí.

La rapidez es una magnitud escalar porque se refiere a un valor independientemente de la dirección y sentido del movimiento. La velocidad es una magnitud vectorial: además del valor de la rapidez, también incluye a la dirección y al sentido del movimiento. 

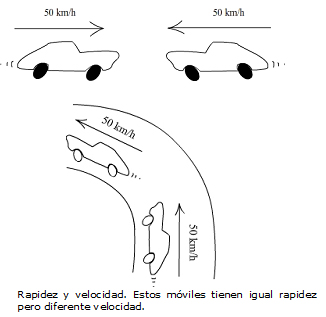
Si miran el siguiente esquema, los cuatro coches en movimiento tienen la misma rapidez (50 km/h) pero sus velocidades son distintas porque comparando la dirección de los dos coches en el dibujo de abajo, o el sentido de ambos en el dibujo de arriba, son distintos. No es que las velocidades sean distintas porque una sea mayor o menor que la otra, en este caso son iguales en valor numérico (50 km/h). Son distintas porque difieren en la orientación espacial del movimiento (los coches van “para lados distintos”).