Lenguaje matemático - EnlaceUBA

Debemos tener en cuenta que los ejemplos de demostraciones que vimos no constituyen una clasificación exhaustiva ni pretenden serlo en la práctica. Mientras que la comunidad matemática acepte una argumentación como válida esta será una demostración. Para complementar esto veamos la siguiente proposición que tiene una interesante demostración.

Demostración. Tomemos el número $\sqrt{2}$; sabemos que este número es irracional. Consideremos el número:

$p = \sqrt{2}^{\sqrt{2}}$

El número $p$ o bien es racional, o bien es irracional. Analicemos cada uno de estos casos:

• Si el número $p$ es racional, la proposición queda demostrada, ya que $a = b = \sqrt{2}$ cumplen lo afirmado en ella.
• Si el número $p$ es irracional, podemos considerar entonces el número $(\sqrt{2}^{\sqrt{2}})^{\sqrt{2}}$. Por propiedades de potencias, usando que $\sqrt{2} \cdot \sqrt{2} = 2$, queda:

$(\sqrt{2}^{\sqrt{2}})^{\sqrt{2}} = \sqrt{2}^{(\sqrt{2} \cdot \sqrt{2})} = \sqrt{2}^2 = 2$

Como $2$ es racional, la proposición queda demostrada tomando en este caso $a = \sqrt{2}, b = \sqrt{2}^{\sqrt{2}}$. Q.E.D.

Lo curioso de esta demostración reside en el hecho de que se considera un número que no se sabe si es racional o no, para luego analizar cada caso por separado, ¡sin saber en ningún momento si el número es racional o no! En cualquiera de los dos casos se logra construir un número que satisface lo pedido. Naturalmente, si se supiera que el número $\sqrt{2}^{\sqrt{2}}$ es racional o no, uno de los dos casos carecería de sentido y su análisis sería innecesario; pero al no saberlo, se torna inevitable el análisis de los dos casos.

Separar en casos de análisis es un método usado en ocasiones para demostrar teoremas. Un conocido caso es el de la demostración del teorema de los cuatro colores, que afirma que todo mapa plano puede colorearse con cuatro colores a lo sumo, de manera que regiones lindantes no posean igual color. Este teorema (conjetura en aquel entonces) fue planteado por Francis Guthrie en 1852 y fue demostrado recién en 1976 por los matemáticos Appel y Haken. El trabajo que realizaron estos matemáticos consistió en “reducir” el problema a 1834 configuraciones diferentes y analizar cada una de ellas mediante un programa de computadora.

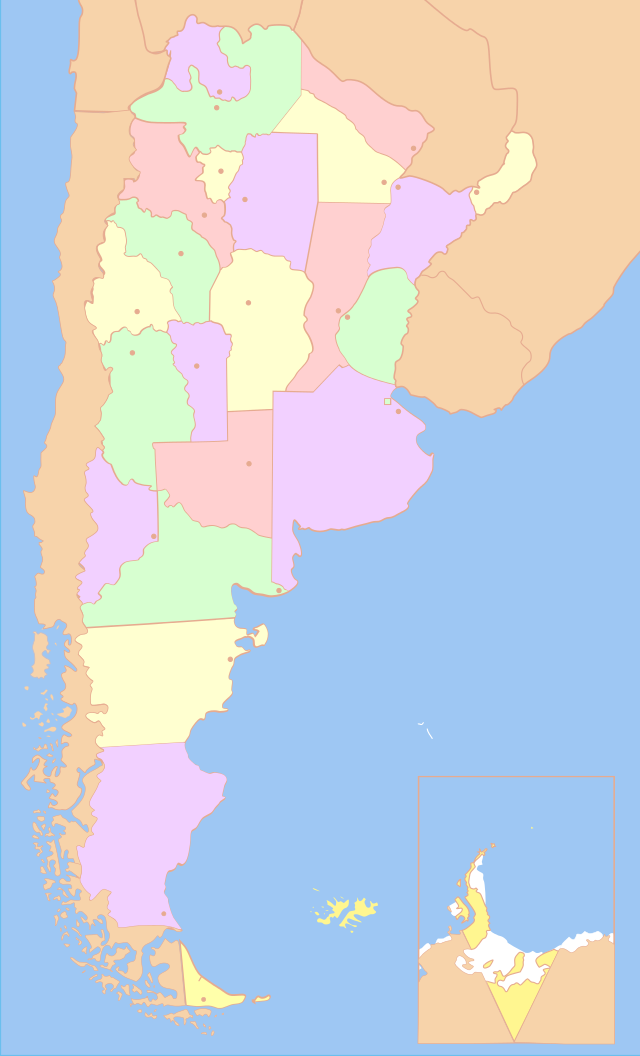
Como ejemplo del teorema de cuatro colores, veamos el mapa de la República Argentina (realizado por el Instituto Geográfico Militar), con sus provincias coloreadas aquí con cinco colores.

De acuerdo al teorema podemos colorearlo con cuatro colores a lo sumo. Notemos que las provincias de Tucumán, Santiago del Estero, Catamarca y Salta son todas colindantes, de modo que será imposible colorear con tres colores o menos. El siguiente mapa muestra una posible coloración con cuatro colores:

A modo de despedida citaremos este teorema que John Conway incluyó en su libro On numbers and games (1976).

Hacé clic para mirar un libro

Como cierre de esta sección, te proponemos realizar la siguiente autoevaluación:

• Autoevaluación